SCAN
(Strongly-Constrained and Appropriately-Normed)
Background
Due to its accuracy and efficiency, density functional theory (DFT) is the choice to calculate electronic structures in chemistry, condensed matter physics, and materials science. In principle, DFT is exact for the ground state electron density and energy. Its exchange correlation energy as a functional of electron density however must be approximated. Accessible properties include electron spin densities, total energy, fundamental energy gap in a generalized Kohn-Sham scheme, and forces on nuclei. Within the adiabatic and classical-nuclei approximations, italso determines vibrational properties of nuclei, and serves as a foundation for ab initio molecular dynamics. DFT was popular in condensed matter physics from the early days of the local density approximation (LDA), and then in quantum chemistry after generalized gradient approximations (GGAs) and hybrid GGA were introduced. Along with its successes however come challenges to DFT, among which is to describe with simultaneous accuracy various types of bonds forming between atoms and molecules with strengths ranging from several meV to several eV.
The current standard density functional approximation for materials science is the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA). In a GGA, the exchange-correlation energy density at a point in space is constructed from the local electron spin densities and their gradients. The PBE was constructed in 1996 to satisfy 11 exact constraints (bounds, scaling relations, and limits) for all possible densities. Its uniform-gas limit would now be called an appropriate norm. In 2014, the PBE paper was identified as the 16th most-cited scholarly article of all time in all fields, showing the wide usefulness of constraint-based functionals.
What is SCAN?
The SCAN (strongly-constrained and appropriately-normed) meta-GGA, which adds the orbital kinetic energy density of each spin to the ingredients list, was constructed in 2015 to respect all 17 known exact constraints that a meta-GGA can satisfy. Because of the high flexibility of a function of 6 variables, SCAN was also fitted to additional appropriate norms, non-bonded systems such as atoms in which it can be accurate for the exchange and correlation energies separately, and not just for their sum as in bonded systems. Without being fitted to any bonded system, SCAN accurately predicts diverse kinds of bonding, including even the effects of intermediate-range van der Waals interaction. (Long-range corrections are available.)
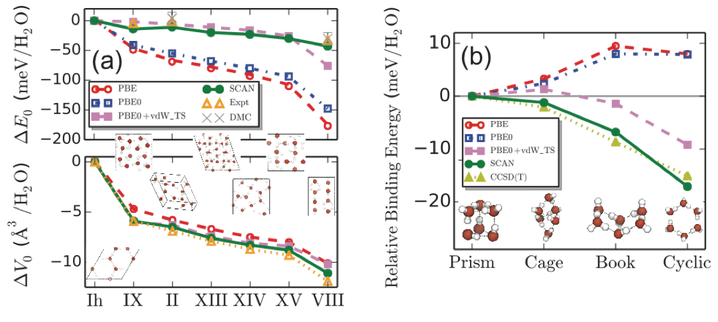
SCAN remarkably captures the intermediate range, many-body vdW interactions necessary for a quantitative description of various ices and gas-phase water hexamers. Left figure (a): relative lattice energy, ∆E0, and equilibrium volume change, ∆V0, per water molecule of seven hydrogen-ordered ice phases with respect to the ground state ice Ih. SCAN is the only functional tested that predicts the relative stability of ice phases in quantitative agreement with experimental results. Bottom figure (b): relative binding energy per water molecule of four low-energy water hexamers. The agreement between SCAN and CCSD(T) shows that SCAN is the only semi-local density functional approximation that predicts the known energetic ordering of these clusters. [J. Sun et al., Nat. Chem. 8, 831 (2016)].
Success Stories
SCAN works much better than the Perdew-Burke-Ernzerhof (PBE) for defects in semiconductors, surface properties of metals, seven phases of ice, liquid water, liquid and supercooled silicon, subtle structural distortions in ferroelectrics, the formation energies andstructural predictions for solids including transition-metal oxides, and the critical pressures for structural phase transitions in semiconductors. SCAN is the only density functional that correctly predicts the band gap (or absence thereof) and the spin moments of the undoped and doped cuprate high-temperature superconductor materials, without free parameters. At a typically much lower computational cost, and without empiricism, SCAN does some things better than the hybrid functionals that mix fractions of GGA and exact exchange.
Unique Features
SCAN meta-GGA and SCAN+rVV10:
- Accuracy
- Computational efficiency
- Robustness
- Best existing density functional for 2D layered materials
- Only density functional that correctly predicts band gap and spin moments of cuprate high-temperature superconductor materials
- Only density functional which reproduces RPA inter-layer binding energies.
Potential Impact
- New, accurate, and widely useful methods of electronic structure theory
- More reliable predictions for the materials-by-designproblem
- Innovative materials for clean-energy technologies
- Broad impact on chemistry, condensed matter physics, and materials science
SCAN predicts accurate geometries and energies of diversely-bonded molecules and materials (including covalent, metallic, ionic, hydrogen, and van der Waals bonds), significantly and systematically improving at comparable efficiency over its predecessors, the GGAs.